HOME BACK

CIRCLE

Main Menu > Circle

CIRCLE

DEFINITION

A circle is a 2D shape that has a closed curve consisting of all points at a FIXED distance from its center.

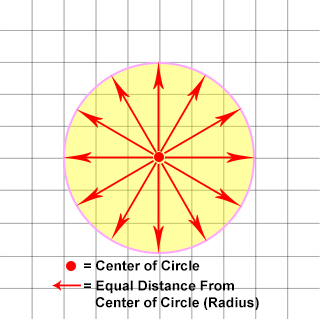
A drawing of a circle showing a center point and radii extruding from center to points on circle.

IT IS HELPFUL TO THINK...

It is helpful to think of a CIRCLE as a SQUARE that has:

  • "lost" its edges,
  • "rounded" its four corners, or
  • "dropped" about twenty percent (20%) of its weight.

TRADITIONAL FORMULA

AreaCircle = πr2 or 3.14 x radius2 or
AreaCircle = ¼π x diameter2

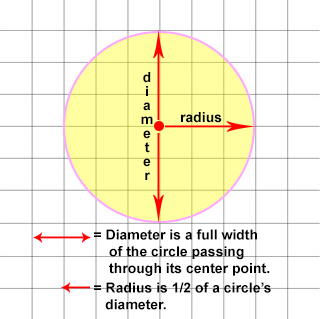
A drawing showing a circle with the diameter and radius measurements inside of the circle.

DEFINITIONS:

  • Pi (π) is the ratio of the circumference of any circle to its diameter or better stated "the circumference divided by its diameter (circumference/diameter)." It is always 3.141592654...
  • The DIAMETER is the distance across a circle through its center.
  • ClThe RADIUS is HALF of the circle's diameter.

THINKING INSIDE THE BOX METHOD

NOTE: The circle is the most difficult 2D shape to explain and to demonstrate because is does not fit "neatly" inside of a box because it does not have any straight sides or any angles. This is why is is discussed last.

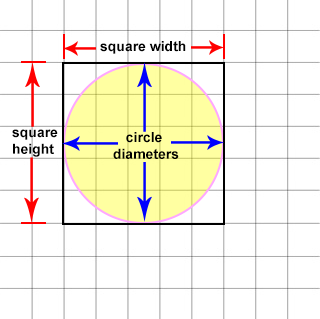
If you place a CIRCLE inside of a box (a square but NOT a rectangle),

  1. You can easily recognize the horizon and vertical circle's diameters (blue arrows) are the same as the height and width of the square (red arrows) that surrounds the circle.

    A drawing showing a circle inside of a box with the width and height of the box matching the width and height of the circle (or its vertical or horizontal diameters)
  2. If you further take notice, you will recognize the circle's area is almost the same as the square area except for the four small edge areas (highlighted in yellow). Notice that the smaller the circle the better it is the see that it is almost the area of a square.

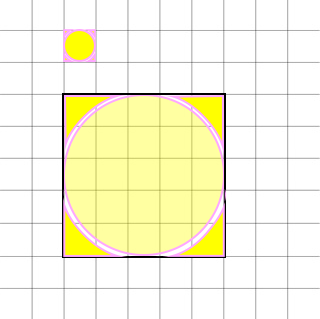
    A drawing showing a circle with the four edges highlighted when placed inside of a box.
  3. If you were to perform calculations on the circle and the square, you will discover the circle's area is about 78.9% (approx. 80%) of the square's area with the four edges making up about 5% each or about 20% total.

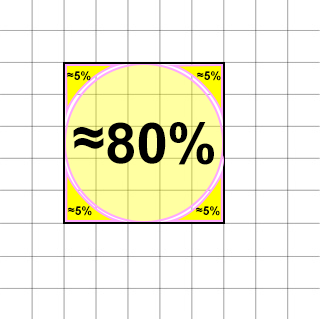
    A drawing showing a circle represent about 80 percent of a square when it is placed inside it. Also, each edge is represent about 5 percent each.
  4. While it is harder to see the square units like the other 2D shapes (quadrilateral or triangle) because it is a circle and not a square, the demo example below makes up about 20 of the 25 squares of the box or roughly eighty percent of 25 (0.80 x 25 = 20).


KEY: Since a circle can be thought of as a square that has lost its four "edges" when placed in a box, instead of having to learn another formula (AreaCircle= πr2), treat the diagonal as BOTH the width and height and use the rectangular formula (height x width) instead and then MULTIPLE THE RESULT BY 0.8 to get an ESTIMATE of its area. See STEP-BY-STEP SOLUTION for detail example.

STEP-BY-STEP DEMO SOLUTION

A circle with a diameter of 5 in has an area of:

  1. Treat the diameters as both the height and the width.
  2. Multiply the diameter by itself (5 x 5) or 25 to get the total area of the square around the circle.
  3. Multiply the total area of the square by 0.80 (80%) to get an approximate area of the circle
    or
    Subtract 20% from total (.20) area of the square to get an approximate area of the circle.

AreaCircle is approximately 25 x 0.80 = 20 in2 or
AreaCircle is approximately 25 - (.20 x 25) = 25 - 5 ≈ 20 in2

NOTE: The symbol ≈ represents approximate value not exact value.

MEMORIZATION TIP

Since a circle is in a "circle" or class by itself, there is only one type of circle and it does not compare to any of the other 2D shapes. Hence, there is no need for a memorization tip.

Close

Circumference (from Latin circumferentia, meaning "carrying around") is the linear distance around the edge of a closed curve or circular object — Wikipedia. The formula is: C = πr or 3.1415 x radius.

Close

Ratio is the relation between two similar numbers with respect to the number of times the first contains the second. In the case of a circle, the ratio is between the circumference and diameter. If the diameter is one, you would have to "stretch" 3.14 diameter lengths around a circle to cover the distance of its circumference. If the diameter is two, you would have to "stretch" 6.28 diameter lengths (6.28/2 = 3.1415). The ratio is always Pi (π) or 3.1415 regardless of the size of the circle.