HOME BACK

QUADRILATERAL

Main Menu > Quadrilateral > Kite

KITE

DEFINITION

A kite is a quadrilateral that has TWO (2) PAIRS OF EQUAL ADJACENT SIDES THAT ARE EQUAL IN LENGTH.

A drawing showing a kite that has two pairs of equal ADJACENT sides that are equal in length.

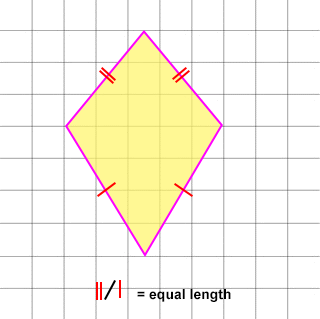
INTERESTING FACTS:

  • A kite sometimes looks like an old fashion kite. Hence, a familiar term is a “box kite.”
  • When all sides have equal length, the kite will also be a rhombus.
  • When all angles are right angles (90°), the kite will also be a square.


IT IS HELPFUL TO THINK...

It is helpful to think of a KITE as a RECTANGLE or SQUARE with its four (4) edges folded into a shape of a kite, a diamond (rhombus) or a box (square).

Close

A box kite is a high performance kite,
noted for developing relatively high lift;
it is a type within the family of cellular
kites. The typical design has four
parallel struts. The box is made rigid
with diagonal crossed struts. (Wikipedia)

Close

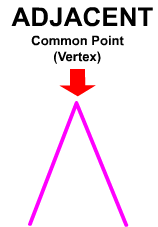
Sides are said to be
adjacent when they
share a common
endpoint.


TRADITIONAL FORMULA

AreaKite = (d1 x d2)/2

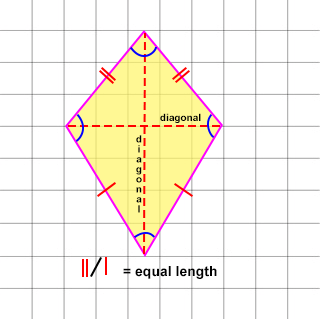
A drawing showing a kite with two diagonals in it.

DEFINITION: The DIAGONALS are lines (dashed) that cross at right angles, and one of the diagonals bisects (cuts equally in half) the other.


NOTE: Angles are equal where two pairs meet.

THINKING INSIDE THE BOX METHOD

If you place a KITE inside of a box, you get a “box kite” (just kidding - smile).

If you place a KITE inside of a box (a rectangle or a square) and then,

  1. CUT the kite down one of its diagonal
  2. CUT half of the other diagonal
  3. FOLD the right or left side that are separated by a diagonal into the opposite side
  4. FOLD the other section to create a rectangle or square that is HALF of the box that it is in

KEY: Since a kite can be thought of as HALF of a rectangle or square when placed in a box, instead of having to learn another formula (AreaKite = (d1 x d2)/2)), use the rectangular formula (height x width) instead. Treat the two diagonals as the width and height and then DIVIDE THE RESULT BY TWO to get its area. See STEP-BY-STEP SOLUTIONS for detail examples.

STEP-BY-STEP DEMO SOLUTIONS

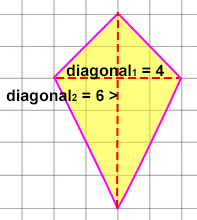
A kite with diagonals of 4 in and 6 in has an area of:

  1. Treat the two diagonals as the height and width of a rectangle.
  2. Use the rectangle formula instead (AreaKite = height x width).
  3. Divide the result by 2.

AreaKite = (4 in × 6 in)/2 = 24 in/2 = 12 in2


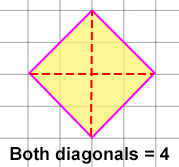
A kite with both diagonals of 4 in has an area of:

  1. Treat the two diagonals as the height and width of a rectangle.
  2. Use the rectangle formula instead (AreaKite = height x width).
  3. Divide the result by 2.

AreaKite = (4 in × 4 in)/2 = 16 in/2 = 8 in2

CAUTION: Like a rhombus, if a kite is a square, you may be tempted to use the height and width of the square as its diagonals. This would be wrong to do. You need to ascertain its diagonals instead by using the Pythagorean Theorem (c2 = a2 + b2).


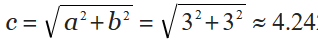
AreaKite = (4.24 in × 4.24 in)/2 ≈ 18 in/2 ≈ 9 in2


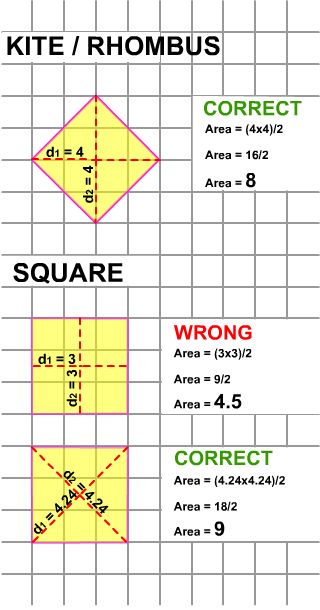
Notice that the area of the square (which can be a kite) is 9 in2 instead of 4.5 in2. You could have just as easily used the square formula (S2) or the more common rectangular formula (height x width) that has been used in this app to determine the area.

MEMORIZATION TIP

To remember the similarities between a kite and a triangle, it is helpful to think of a KITE or a TRIANGLE as HALF of a rectangle or a square. Hence, you divide the result by two.