Main Menu > Quadrilateral > Parallelogram > Rhombus
RHOMBUS
DEFINITION
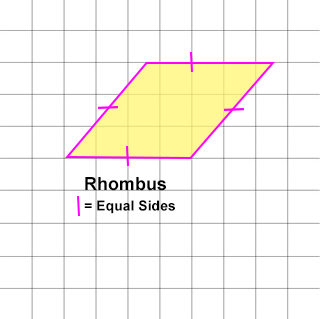
A rhombus is a quadrilateral / parallelogram that has FOUR (4) EQUAL SIDES but not necessarily right angles (90°) like a square or a rectangle.
A right angle is an internal angle which is equal to 90°.
INTERESTING FACTS:
- Because a rhombus is a parallelogram like a rectangle or square, opposite sides are parallel, and opposite angles are equal.
- Any SQUARE is a RHOMBUS, but not all RHOMBUSES are SQUARES.
- Every RHOMBUS is a PARALLELOGRAM and a KITE.
- A RHOMBUS with all right angles is a SQUARE.
- Hence, a RHOMBUS can go by many names and shapes:
- Rhomb
- Diamond
- Kite
- Square
- Equilateral Quadrilateral (Equilateral - Four equal sides; Quadrilateral - Four sides)
- The word RHOMBUS comes from a Greek word which means "something that spins" like the old fashion spinning tops:

Notice the shape of some of the spinning tops looks similar to the rhombus shape.
IT IS HELPFUL TO THINK...
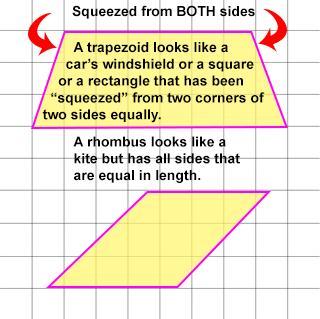
It is helpful to think of a RHOMBUS as a SQUARE or a RECTANGLE that has been pushed from a side so that all its sides are equal in length.
TRADITIONAL FORMULA
Formula 1:
Formula 2:
DEFINITIONS:
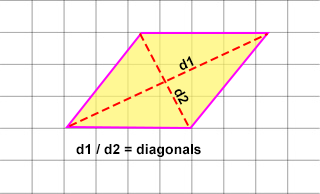
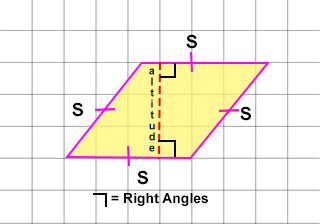
- The ALTITUDE is the distance at right angles to two sides of a rhombus.
- The DIAGONALS are lines that cross at right angles, and one of the diagonals bisects (cuts equally in half) the other.
THINKING INSIDE THE BOX METHOD
If you place a RHOMBUS inside of a box (a rectangle or a square) and then,
- CUT one side of the rhombus from the highest point on the rhombus to form a right triangle
- MOVE the right triangle up and across to the opposite side of the rhombus and move it into place to create a rectangle or a square
If all sides of the rhombus are equal and if you place a RHOMBUS inside of a box (a square but NOT a rectangle) and then,
- CUT the rhombus down one of its diagonal
- CUT half of the other diagonal
- FOLD the right or left side that are separated by a diagonal into the opposite side
- FOLD the other section to create a rectangle or square that is HALF of the box that it is in
KEY: Since a rhombus is basically a square that has been "slanted," it can still be treated somewhat like a square. So, instead of having to learn another formula (AreaRhombus = altitude × S), treat the altitude as the height and S as the width and simply use the rectangle formula (height x width) instead. See STEP-BY-STEP SOLUTIONS for detail examples.
STEP-BY-STEP SOLUTIONS
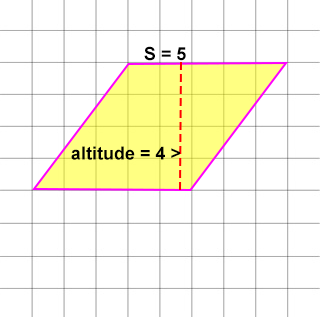
A rhombus with an altitude of 4 in and a side of 5 in has an area of:
- Treat the altitude as the height and S as the width of a rectangle.
- Use the rectangle formula instead (AreaRhombus = height x width).
AreaRhombus = 4 in x 5 in = 20 in2
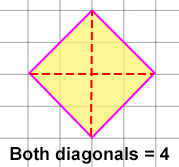
A rhombus with both diagonals of 4 has an area of:
- Treat the diagonals as the height and width.
- Use the rectangle formula instead (AreaRhombus = height x width).
- Divide results by 2.
AreaRhombus = 4 in x 4 in = 16 in2/2 = 8 in2
CAUTION: Like a kite, if a rhombus is a square, you may be tempted to use the height and width of the square as its diagonals. This would be wrong to do. You need to ascertain its diagonals instead by using the Pythagorean Theorem (c2 = a2 + b2).
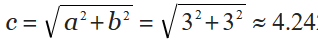
AreaKite = (4.24 in × 4.24 in)/2 ≈ 18 in/2 ≈ 9 in2
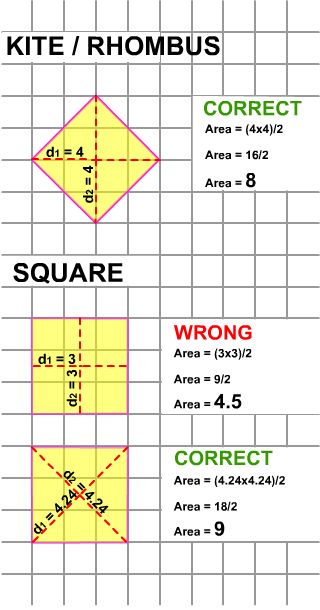
Notice that the area of the square (which can be a rhomubus) is 9 in2 instead of 4.5 in2. You could have just as easily used the square formula (S2) or the more common rectangular formula (height x width) that has been used in this app to determine the area.
MEMORIZATION TIPS
- To help you remember the shape of a rhombus, you can think of it by its other more descriptive name of diamond because of its shape instead of the unusual name of rhombus.
- To help remember the different between a trapezoid and a rhombus shape, think of a trapezoid as looking at the back of a car's windshield and think of a rhombus as a slanted box that has been stretched so that all sides are equal.